12.1全等三角形
(1)全等形
解:能够完全重合的两个图形叫做全等形。
(2)全等三角形
解:能够完全重合的两个三角形叫做全等三角形。
(3)全等三角形的对应顶点、对应边、对应角
解:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点。
重合的边叫做对应边。
重合的角叫做对应角。
(4)全等三角形的性质
解:对应边相等,对应角相等。
12.2三角形全等的判定
(1)三角形全等有哪几个判定条件
解:①三边分别相等的两个三角形全等。(简写“边边边”或“SSS”)
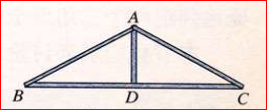


②两边和它们的夹角分别相等的两个三角形全等。(简写“边角边”或“SAS”)
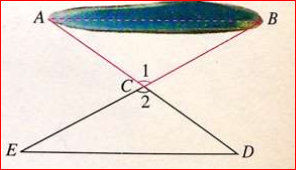

③两角和它们的夹边分别相等的两个三角形全等。(简写“角边角”或“ASA”)
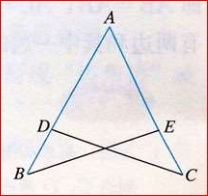


④两角和其中一个角的对边分别相等的两个三角形全等。(简写“角角边”或“AAS”)
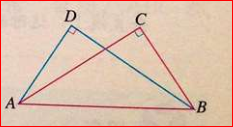
⑤斜边和一条直角边分别相等的两个直角三角形全等。(简写“斜边、直角边”或“HL”)
实际上,这个定理就是三角形全等判定条件的“角角边”,因为直角90°是已知相等的,斜边是直角的对边,
再加上一条直角边相等。


12.3角平分线的性质
(1)角平分线的画法
解:
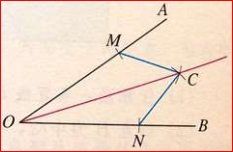
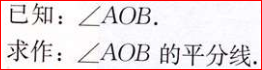

(2)角的平分线的性质
解:角的平分线上的点到角的两边的距离相等。
(3)利用全等三角形证明上面(2)的结论
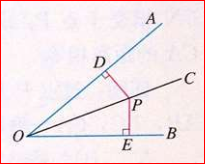
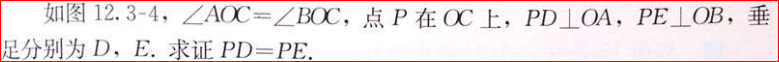

(4)角的内部到角的两边的距离相等的点在角的平分线上。